Deep semi-supervised learning for medical image segmentation:A review

Problem overviews

Problem definition

半监督学习的核心目标即是通过利用大量未标记的数据来提高监督学习的性能。在本文的半监督学习设置中，假设数据集$D$由两部分组成: 标签样本集$D_L=(X_i,Y_i)_{i=1}^L$和无标签样本集$D_U=(X_i)_{i=L+1}^{L+N}$，在这里$X,Y,L,N$分别代表训练原始图像、标签、有标签图像数目、无标签图像数目，半监督分割任务的优化目标为：

$$\begin{aligned}\operatorname*{min}_{\theta}\sum_{i=1}^{L}\sum_{a=1}^{W}\sum_{b=1}^{H}L_{S}(f(X_{i}^{(a,b)}),Y_{i}^{(a,b)};\theta)+\alpha\sum_{i=L+1}^{L+N}\sum_{a=1}^{W}\sum_{b=1}^{H}L_{U}(X_{i}^{(a,b)};\theta)\\+\beta\sum_{i=1}^{L+N}\sum_{a=1}^{W}\sum_{b=1}^{H}R(X_{i}^{(a,b)};\theta)\end{aligned}$$

其中$L_S，L_U$和$R$分别是监督损失、非监督损失和正则化项。$\alpha$和$\beta$表示最后两项余额的系数，$f$和$\theta$是模型及其参数。$W$和$H$分别表示图像的宽度和高度。为了简化表达式，忽略了像素位置$(a,b)$。对于半监督学习，很难在无监督损失项和正则化项之间划清界限。

Method

在这一部分中，结合半监督损失函数和模型设计的最大特点，将深度半监督医学图像分割方法分为五个部分，即pseudo-labeling method、consistency regularization method、基于遗传算法的方法、contrastive learning-based method和hybrid method。对于每种方法，我们首先介绍了损失函数的基本原理和一般形式，然后给出了每种方法的改进。最后，从优势、劣势和可能的发展方向等方面进行了总结。

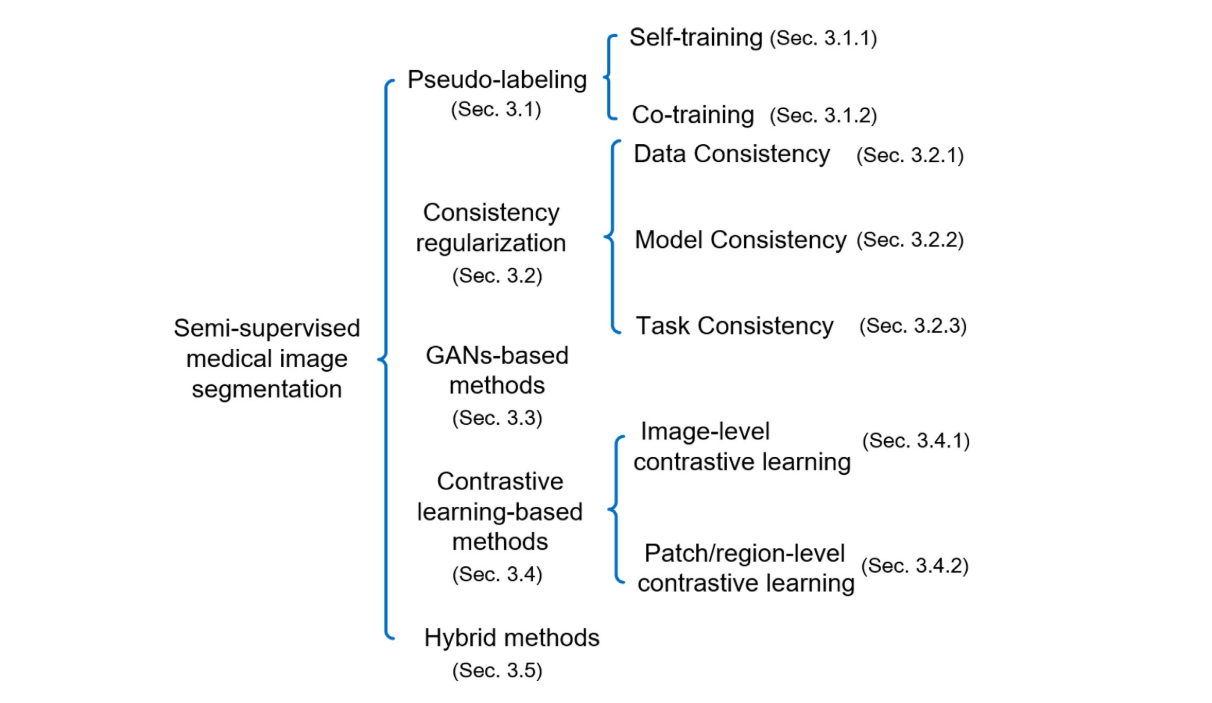
Pseudo-labeling

伪标记方法是一种广泛使用的半监督学习方法。它首先在已标记的数据集上训练一个模型，然后以最大置信度将伪标签分配给未标记的样本。带有伪标签的样本可以扩展已标记的数据集，提高模型性能。自训练(self-training)和协同训练(co-training)是典型的伪标记法。

Self-training

Self-training是Pseudo-labeling的经典方法，它通过在已标记的数据集上预训练一个模型，并通过对未标记数据的预测迭代地重新训练或微调模型本身。损失函数可以表示如下：

$$\min_{\theta}\sum_{i=1}^{L}L_{S}(f(X_{i};\theta),Y_{i})+\alpha\sum_{i=L+1}^{L+N}L_{U}(f(X_{i};\theta),\hat{Y}_{i})$$

其中$\hat{Y}$通常包含有大量噪声的伪标签。如何提高伪标签的质量是self-training算法的核心，虽然其简单易实现，但是当初始的伪标签包含有大量噪声时，会对网络训练产生负面影响，此外，当没有标签数据可用时，使用无监督技术是self-training的一个很好的选择。

Co-training

当只使用一个模型时，self-training的伪标签质量通常差别很大，因此结合多个模型生成更加稳健的伪标签非常重要。

Co-training算法要求数据集中的每个数据都有两个或多个不用但互补的试图，每个视图都足以训练一个好的模型，在每次迭代后，如果当前模型输出的置信度预测的概率高于预设阈值，则将未标记的数据添加到另一模型的训练集，简而言之，一个模型为其他模型的输入提供标签。损失函数可以表示为:

$$$$

其中，$j，v_j，\overline{j}、V$分别代表不同的模型索引、数据的查看操作、非当前模型索引、查看编号

Summary

Self-training方法的核心是提高伪标签的质量。相比之下，Co-training依赖于数据的多个独立特征，因此它将产生更准确和更稳健的结果。协同训练模型通常具有相同的结构和不同的初始化方式。如果共同训练的网络共享相同的参数，这可能会导致较低的性能，因为它们各自的优化目标和梯度下降方向不同。

Consistency regularization

由上一节得知，使用伪标签增加了训练不稳定的风险，因此引入了一致性正则化项(consistency regularization term)以对假设施加先验约束，该假设假定对数据点的实际扰动不应该改变模型的输出。接下来，我们将从数据、模型和任务三个维度对其进行阐述。

Data consistency

一致性正则化通常会对未标注数据进行转换或添加随机扰动，以迫使模型生成更平滑的预测结果。具体而言，数据层面的一致性要求即使输入经过不同变换或扰动，输出结果仍需保持一致。对于某些变换操作，存在逆变换或近似逆变换。换言之，当对未标注输入数据进行变换时，网络输出会应用相应的逆变换或近似逆变换。而随机扰动通常会添加随机噪声。

(Horlava et al., (2020))采用强增强(Cubuk, Zoph, Shlens, & Le(2020))和弱增强（基本几何变换）来处理未标记数据。通过调整结果，可以增强正则化效果。(Xu et al., (2021))设计了两种扩展机制(Shadow-AUG 和 Shadow-DROP)。前者通过在输入超声图像中添加模拟阴影伪影来丰富训练样本，使网络对潜在的阴影伪影具有鲁棒性。而后者的重点是剔除操作(Kendall & Gal, (2017))，前列腺边界是通过使用相邻的无阴影像素的分割网络推断出来的。此外，混合法(Liu、Xiao、Jiang & He, (2022))混合了有标记和无标记的数据，使模型难以记住训练数据，从而能更好地泛化到未知数据。此外，(Qiao et al., (2022))设计了一种不可靠稀释一致性训练机制，通过将可靠的标注数据整合到不可靠的非标注数据中来稀释不可靠度。此外，一些工作还进行了一致性数据转换，如补丁-洗牌数据转换(Li, Peng & Xu, (2023))、剪贴增强(Yap & Ng，(2023))、复制-粘贴(Bai、Chen、Li、Shen & Wang，(2023))。上述方法都提倡配对图像（同一图像的两个增强版本），而很少关注非配对图像（来自不同患者的图像）。为此，(Chen、Zhang、Debattista & Han, (2022))扩展了现有的一致性正则化方法，以保持非配对图像之间的一致性。

数据一致性虽能充分利用数据的丰富信息，但其有效性高度依赖于分布假设——即未标注数据的预测结果必须准确且与标注数据的标签保持一致。然而在实际应用中，由于未标注数据可能包含噪声、错误标注或不确定性，这一假设往往难以成立。

Model consistency

增强模型多样性是一致性正则化研究的另一方向。通常，模型一致性要求同一图像输入不同模型时，输出结果要保持一致。现有工作有多种若干种consistency model，例如\prob模型(Sajjadi、Javanmardi & Tasdizen, (2016))，Temporal Ensembling(Laine & Aila, (2016))和Mean Teacher(Tarvainen & Valpola, (2017))。根据这些模型的数量，大致可以分为single model, dual-model, dual-decoder model，如下图所示。

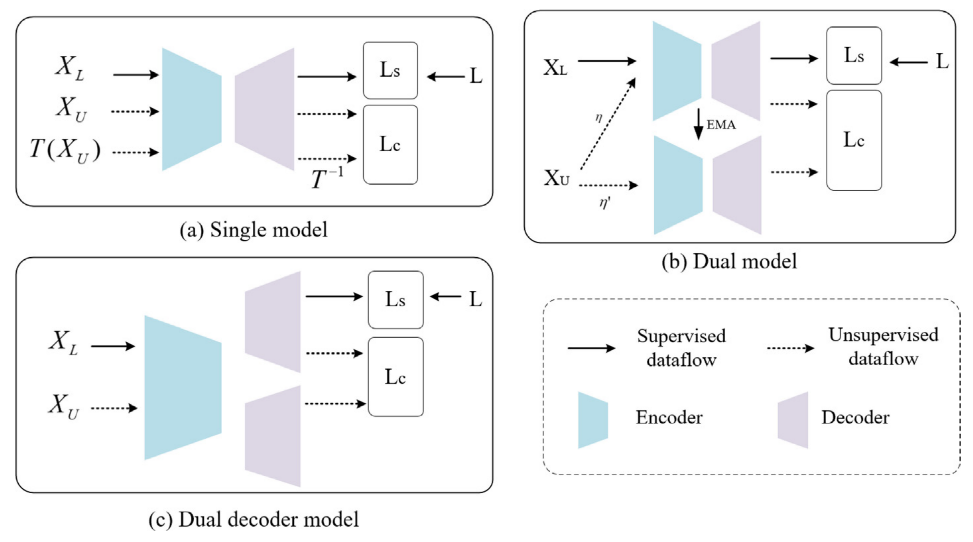
Single model

单模型通过结合变换或随机扰动来实现一致性，如上图(a)所示。损失函数可以表示为：

$$\min_{\theta}\sum_{i=1}^{L}L_{S}(f(X_{i};\theta),Y_{i})+\alpha\sum_{i=L+1}^{L+N}L_{U}(T^{-1}(f(T(X_{i});\theta)),f(X_{i};\theta))$$

在这里$T$和$T^{-1}$分别代表变换和对应的逆变换。

(Peng、 Pedersoli & Desrosiers (2020))通过利用未标记图像分割输出与其变换输出之间的KL一致性扩展了互信息正则化。 (Cao et al., (2020))提出了一种用于乳腺肿块分割的时间域集成分割模型。注意到网络在不同尺度输出的不一致性也可视为一种扰动。例如，Uncertainty Rectified Pyramid Consistency(URPC) (Luo et al., (2022))利用金字塔一致性来测量不同尺度输出的不确定性，从而获得更准确和稳健的分割结果。

Dual model

Mean Teacher(Tarvainen & Valpola，(2017))采用指数移动平均(EMA)在训练过程中对模型权重进行平均。相较于直接使用输出预测，这种方法往往能够生成更精确的模型。dual model如上图(b)所示，其优化目标函数为

$$\min_{\theta}\sum_{i=1}^{L}L_{S}(f(X_{i};\theta),Y_{i})+\alpha\sum_{i=L+1}^{L+N}L_{U}(f(X_{i};\theta^{\prime},\eta^{\prime}),f(X_{i};\theta,\eta))$$

其中$\theta$和 $\theta'$分别为学生模型和教师模型的参数，$\eta$和$\eta'$为随机噪声（如高斯噪声等）。

为了提高教师模型输出结果的质量，在Mean Teacher框架中集成了不确定性方法(Chang, Yan, Lou, Axel, & Metaxas, (2020); Hang et al., (2020); Li, Yu et al., (2020); Lu, Yin, Fu, & Yang, (2023); Wang et al., (2020); Yu, Wang, Li, Fu, & Heng, (2019))，通常包括两种扰动方案：数据转换（如旋转、缩放等）和网络剔除操作。此外，还有一些著作引入了重构一致性(Chen，Zhou，Wang and Xiao，(2022))、多尺度一致性(Wang，Wang et al., (2022))、先验解剖([Chen et al., (2023)])()、切片间一致性(Zeng et al.，(2023))来提高师生模型的一致性。然而，Mean Teacher框架有一个缺点，即通过EMA 更新参数，导致教师模型和学生模型紧密耦合(Ke, Wang, Yan, Ren, & Lau, (2019))。此外，(Huang、Chen、Chen、Lu & Zou(2023))鼓励主模型从两个辅助模型中学习一致性。

Dual-decoder model

该模型由一个共享编码器和两个略有差异的解码器组成。如图2©所示，这两个解码器通常具有相同的结构但不同的初始化参数，其损失函数如下：

$$\min_{\theta_1} \sum_{i=1}^L \sum_{j=1}^2 L_S(D_j(E(X_i)), Y_i) + \alpha \sum_{i=L+1}^{L+N} L_U(D_1(E(X_i)), D_2(E(X_i)))$$

其中$E$、$D$和$j$分别代表编码器、解码器和解码器的索引。

代表作（Fang & Li，2020；Wu，Ge et al.，2022；Wu，Xu，Ge，Cai and Zhang，2021）采用双解码器或多解码器，产生多个不同的输出。每个解码器可以在另一个解码器的监督下学习（Fang 和 Li，2020 年），或最小化两个或多个解码器之间的统计差异，以减少模型的不确定性（Wu，Ge 等，2022 年；Wu，Xu 等，2021 年），这与交叉伪监督（CPS）模型的主要思想相似（Chen，Yuan，Zeng，& Wang，2021 年）。此外，为了缓解认知偏差，相互校正框架（MCF）（王晓、毕、李和高，2023）引入了两个不同的子模型，探索并利用子模型之间的差异来校正模型的认知偏差。

代表性研究(Fang & Li, 2020)；Wu，Ge et al., (2022)；Wu，Xu，Ge，Cai and Zhang, (2021))采用双解码器或多解码器架构，生成多种不同输出。各解码器可通过其他解码器的监督学习(Fang & Li, (2020))，或通过最小化两个及以上解码器间的统计差异来降低模型不确定性(Wu，Ge et al., (2022)；Wu，Xu et al.，(2021))，这与交叉伪监督(CPS)模型的核心思想(Chen，Yuan，Zeng，& Wang，(2021))异曲同工。此外，为缓解认知偏差，互校正框架(MCF)(Wang, Xiao, Bi, Li and Gao, (2023))引入两种不同子模型，通过探索并利用子模型间的差异来校正模型的认知偏差。

Task consistency

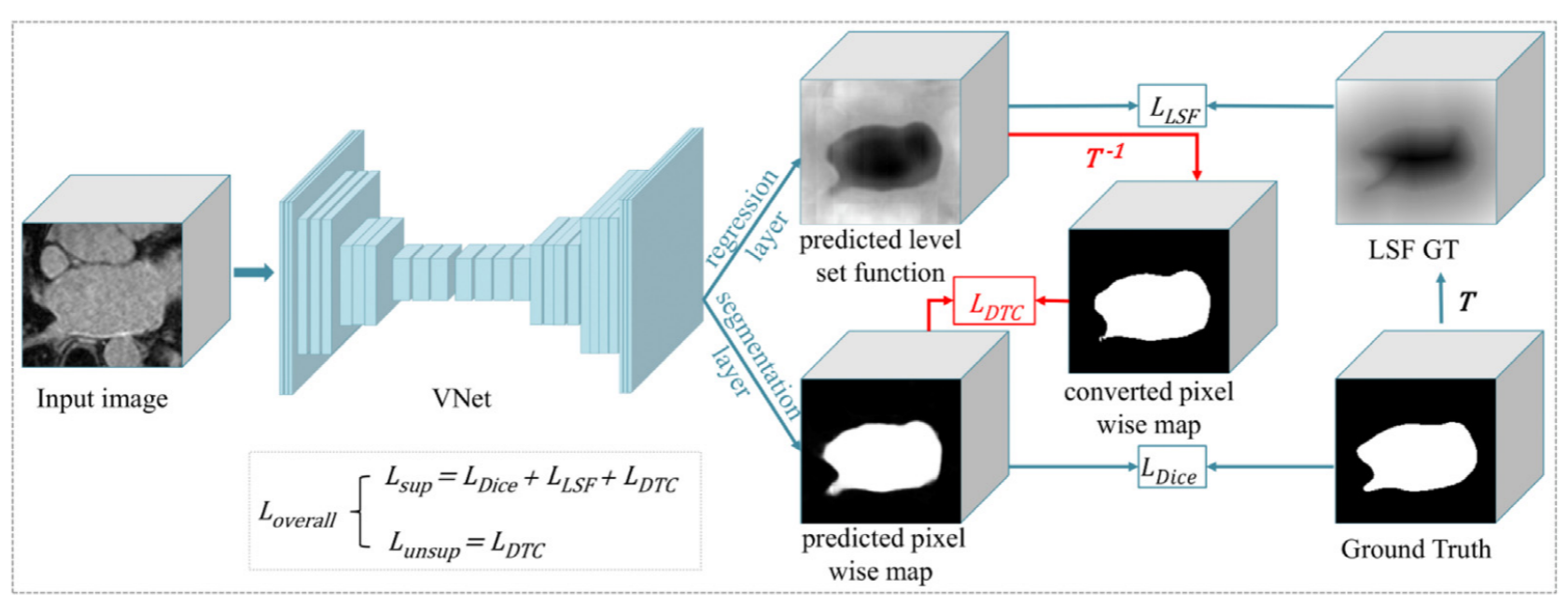
上述工作只考虑了不同扰动和变换下输入的一致性，忽略了不同任务之间的一致性。由于原始数据包含更多信息，因此可以设计多任务或其他辅助任务进行半监督学习。最近，(Zamir et al., (2020))在推理路径不变性的基础上利用了跨任务一致性，表明研究任务一致性非常有利。图3显示了任务级一致性正则化的过程。损失函数可总结如下。

$$\min_{\theta_1,\theta_2} \sum_{i=1}^L\sum_{j=1}^2 L_S(f_j(X_i;\theta_j),Y_{ij}) + \alpha \sum_{i=L+1}^{L+N} L_U(f_1(X_i;\theta_1),T^{-1}f_2(X_i;\theta_2))$$

其中$\theta_1$,$\theta_2$和$j$分别代表分割网络参数、其他任务网络参数和任务索引。$T^{-1}$是不同任务间输出的逆变换。

(Kervadec、Dolz、Granger & Ben Ayed, (2019); Luo et al., (2021); Wang、Zhan et al., (2022))介绍了回归任务，这不仅对分割网络进行了正则化，还迫使未标注数据预测与推断的标签分布相匹配。(Zhang、Liu、Yu & Li, (2021))设计了一个具有分割和病变区域修复功能的双任务网络，其中未标记的数据由掩蔽病变区域的修复损失引导。(Lyu、Sui、Wang、Dou & Qin(2023))利用重建任务从图像中捕捉解剖信息并改进分割任务。(Chen、Sun、Wei、Wu & Ming, (2022))设计了一种特定类别知识提取策略，从已标记图像到未标记图像的上下文和结构亲和特征中转移特定类别知识。上述方法虽然可以借助辅助任务提高网络性能，但也存在计算开销大、超参数调整困难等问题。

Summary

数据一致性在很大程度上依赖于数据假设，如果数据维度过高，扰动效果无疑会很低(Verma et al., (2022))。此外，这种方法通常不利于不同模型之间的知识交流，导致每个模型都容易过度拟合(Feng et al.,(2022))。对于网络扰动，即使用丢弃操作来获取不确定性的模型(Wang et al.,(2020))，由于每次迭代需要多次前向传播来获取不确定性，计算成本较高。(Aralikatti、Pawan & Rajan, (2023))将数据级扰动和网络级扰动集合起来，在模型预训练阶段集成数据级扰动，然后在微调阶段集成模型级扰动。

在模型一致性方面，由于单网络的参数更新方式相对简单以及串行训练的不稳定性，通常无法获得有竞争力的结果，而双模型通常不会遇到这个问题。双解码器模型既能保持模型多样性，又能节省GPU显存。此外，对于平均值教师及其变体，通常会在训练数据中添加各种扰动。控制变化强度至关重要。如果变化太弱，可能会出现 "懒学生 "现象(Huo et al.,(2021))，从而给学习模型带来较大的波动。相反，较大的图像扰动可能会拉大师生之间的成绩差距，学生可能会失去学习动力，影响分割成绩。

与多任务学习不同，分割任务的样本通常只有掩码标签。在这种情况下，可以将分割掩码转换成带符号的距离域(SDF)或带符号的距离图(SDM)，作为回归标签来构建回归任务。但其局限性在于，SDM(SDF)图只能描述每个体素到对象边缘的距离。当存在多个类目标时，背景中的体素的距离定义将是模糊的，因此 SDM(SDF)并不适合这种情况。